fugu, the generalised relu activation function

Posted on June 6, 2018 by Noon van der Silk

Recall the standard ReLU function from neural networks:

$$ \texttt{ReLU}(x) = \max(0, x) = \begin{cases} x & x > 0 \\ 0 & \text{otherwise} \end{cases} $$

All well-and-good. But what if I want to apply a function to the lower-half of this function, instead of setting it to 0? Infact, what if I want to apply a function to the top-half as well! And while we’re at it, why should the inflexion point be 0 always?

So, here’s the fugu function:

$$ \texttt{fugu}(x, f, g, p) = \begin{cases} g(x) & x > p \\ f(x) & \text{otherwise} \end{cases} $$

Then, ReLU(x) = fugu(x,0,id,0), if you wish.

Here’s the fugu function in Python TensorFlow:

def fugu (x, f, g=lambda x: x, point=0):
    cond   = tf.less(x, point)
    return tf.where(cond, f(x), g(x))

There, tf.nn.relu(x) = fugu(x, tf.zeros_like).

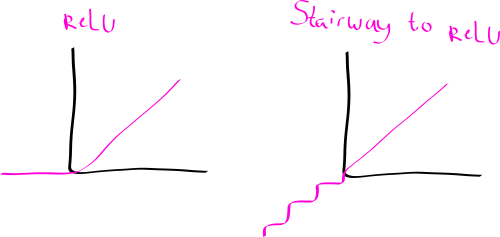
What kinds of cool/useful functions can you build with this?

Exercise: Can you use the fugu function to build a kind of “stairway-to-relu” function?