Happy Haskmas!

Posted on December 18, 2015 by Noon van der Silk

At the last Melbourne Haskell Meetup we got into the spirit by making Christmas trees in Haskell.

However, I recently have access to a 3D printer, and I’ve long wanted an excuse to try and use ImplicitCAD, so I set about trying to make a 3D version of Lyndon’s logo.

So of course, I love stack I created a new simple project with stack new and got started.

It turns out that ImplicitCAD has a pretty nice and reasonably intuitive interface (similar to the code that one would write into OpenSCAD).

I built the 3D version of the logo by moving around rectangles, and by extruding a hand-drawn shape.

The cool thing about generating this image in fully-feature programming language is that I can build a tree of any size I like!

Here’s the (pretty verbose) code that gets me a tree of arbitrary depth:

ntree :: Integer -> SymbolicObj3
ntree n = finalObj
  where
      dec     = 0.8
      ratios  = 0 : [dec^j | j <- [0..(n-2)]]
      -- build up logo structure
      ((lx, ly, lz), objs) = foldl f ((0, 0, 0), []) (zip [0..(n-1)] ratios)
      -- position of logos
      (x,y,z) = (40, 4, 0)
      f :: ((ℝ, ℝ, ℝ), [SymbolicObj3]) -> (Integer, Float) -> ((ℝ, ℝ, ℝ), [SymbolicObj3])
      f ((x', y', z'), xs) (j, r) =
                let newPos = (x' + r*x, y' + r*y, z' + r*z)
                    s      = dec ^ j
                    loc    = if (even j) then R else L
                    obj3   = translate newPos $ scale (s, s, s) (logoBauble loc)
                 in (newPos, obj3 : xs)
      -- star
      (a,b,c)   = (40.5, 24.5, 0)
      starScale = dec ** (fromIntegral (n-3))
      posScale  = dec ** (fromIntegral n)
      starObj   = translate (lx + (posScale * a), ly + (posScale * b), lz + (posScale * c))
                    $ scale (starScale, starScale, starScale) star
      finalObj = union (starObj : objs)

Running this with n = 5 gives result in the following render in OpenSCAD:

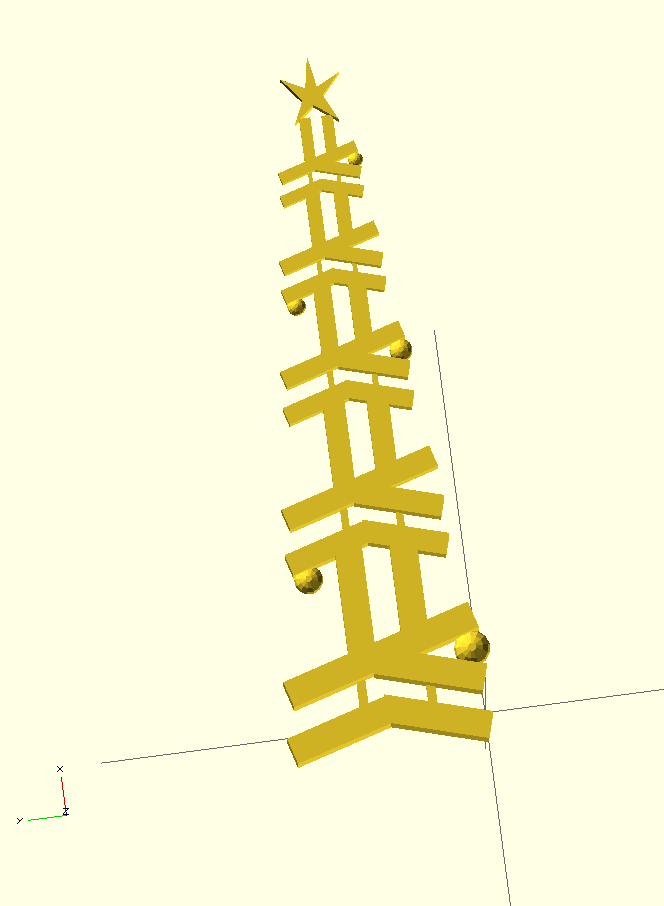
So there you have it! You can view the source code here: github.com/silky/haskmas or download a ready-to-print STL from Thingiverse.

Have a happy Haskmas! :)